Det Gyldne Tårn - The Golden Tower
Slowly you move up the tower. The ground is far below, and you still have a long way to go. During 20-25 seconds, the lift moves with nearly constant velocity to the highest point, about 60 m up. What forces act on you during this part of the ride?
Movie of the Golden Tower from Tivoli - and an Easter version
The graph below shows accelerometer and elevation data for the ride.
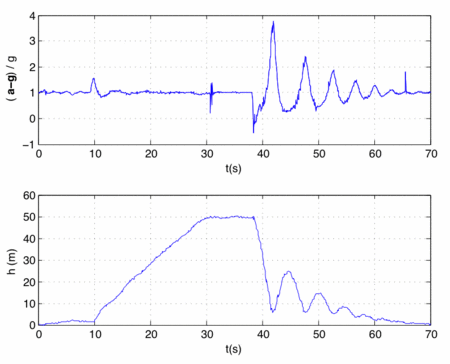
- At the top, you have about 7-10 seconds to enjoy the view. The downhill motion starts: You are "shot" down, accelerating nearly twice as fast as during free fall. What are the forces on you during this part of the ride? Use the accelerometer graph to draw an approximate graph over velocity and elevation as a function of time, and mark the different parts of the ride. Do you ever experience weightlessness?
- The fall lands on pressurized air, and a few up- and down bounces. During the first bounce, the accelerometer graph shows that you experience nearly 4g. What are the forces acting on you in that moment? What is your acceleration? Are there moments when the velocity is zero? At what times does the velocity have a maximum? Minimum (i.e. when is it most negative)?
To draw these and other graphs: Download the data, which can be used e.g. in spreadsheet programs or in matlab. You may want to look closer at acceleration and velocity during the start of the ride, or as you are shot down, pr during the final bounces. You may have to make small adjustment to the acceleration data to ensure that the velocity approaches zero at the end of the ride. How large is the adjustment? How does it compare to the uncertainty in the data? (Data sheet for the sensor.) You may also compare the results for this ride to other Turbo Drop rides, such as the Höjdskräcken found at Liseberg until 2015.
Hor far away is the horizon?
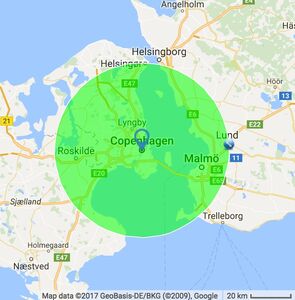 How far can you see from the top? Can you see Malmö? Landskrona? Ven? Roskilde? Elsinor?
How far can you see from the top? Can you see Malmö? Landskrona? Ven? Roskilde? Elsinor?
On the Tivoli movie from The golden tower, you can see the sea. How far away is the horizon when you are 60 above sea level? Use Pythagoras' theorem, with R=the radius of the Earth, D= distance to the horizon and h= elevation above sea level.
This gives (R+h)2=R2 + D2. Since h is much smaller than R, we can neglect h2 and get 2Rh ≈ D2.
- Look at the map, before the visit and try to estimate how far away you should be able to see when you are at the highest point
- You can also try http://www.freemaptools.com/radius-around-point.htm. (The circle in the map to the right is drawn with a radius of 40km around Copenhagen).

